Scientific Challenges and Encryption of Discoveries in the 17th Century Rational Mechanics

Scientific Challenges in the Early Modern Time

Proposing mathematical questions as contests were popular among Renaissance and early-modern mathematicians, including Christiaan Huygens (1629–1695)  and Gottfried Wilhelm Leibniz (1646–1716) . Commonly, a mathematical question was proposed in a journal article, and a few mathematicians were specifically nominated to solve the problem in a given period of time. If the starter of the challenge already possessed the solution, he might have included an encrypted form of the solution when announcing the challenge. Sometimes, nominees solved the problem before the official deadline and wanted to announce their success. In these cases, they would communicate an encrypted form of the solution. The complete solutions had to be submitted to the same journal before the deadline, and the received solutions would be published in the order of submission. Later, review articles and discussions would follow about the quality of the solutions.

What was the reason for encrypting solutions?

Hiding discoveries in ciphers was a common practice in the early modern period. Natural philosophers announced their findings as a cipher to prevent any priority dispute. It was primarily used when making a discovery, but the founder needed more time to perfect it before publishing. In the meantime, if someone else had made the same discovery, the priority could be decided using the anagram as evidence. Therefore, anagrams were used to document scientific conjectures in an age when copyrights and patents were in their early stages and could not testify who discovered something first. Biagioli (2012, 222) asserts that when an anagram is published in a book, it is meant to be the registration of a discovery — a claim of having a claim— because, at this stage, the discovery itself was encrypted and thus inaccessible. Then the author would rejoin the content with its certified temporal origin. Jan Golinski (2005) suggests that writing a cipher could also be for privatizing knowledge. It was a convention used mainly by Robert Hooke (1635–1703) because he believed in private intellectual property ownership. 

We should note that anagrams were also used long before the seventeenth century; for instance, by Roger Bacon (1219–1292). He concealed his discoveries in anagrams for an entirely different reason: to keep secret potentially dangerous findings, such as a recipe to make gunpowder. He wrote:

“You may find (by actual experiment) whether I am writing riddles to you or the plain truth.”

Although the uneducated could not understand his writings, the educated would (Burke, 1927)!

In 1668, John Wallis (1616–1703) suggested that there should be an international standard for the conformity of ciphers so that no one could put a sense to a cipher other than what had been intended by its author. In fact, Huygens had previously suggested a set of rules for this to be witnessed by the Royal Society: anagrams should not exceed sixty letters, can be in 2 or 3 lines or separate sections, and can be in English or Latin (Iliffe, 1992, 36).

Here, I will discuss three different usages of anagrams in two mathematical challenges started by Jacob Bernoulli, the first mathematician of the Bernoulli dynasty. I will also briefly discuss Hooke’s publication of his discoveries as anagrams about the topics related to these two challenges. We will see some differences in these anagrams: in their forms and degree of complexity that closely relate to the way these anagrams were communicated.

Funicularia Challenge: Finding the curvature of a hanging thread

After a dialog with a craftsman in 1687, Jacob Bernoulli (1654–1705)  studied the curvature, strength, flexibility, and elasticity of threads and beams under a load. Between 1687 and 1690, with his brother Johann, he was trying to understand Leibnizian calculus by applying it to known problems of rational mechanics. One of these problems was to find the curvature a thread takes under its own weight when its ends suspend it.

In May 1690, Jacob announced the problem as a mathematical challenge at the end of an article he published in Acta Eruditorum (AE).

“Problema vicissim propenendum hoc esto: Invenire, quam curvam referat funis laxus &  inter duo puncta fixa libere suspensus. Sumo autem, funem esse lineam in omnibus suis partibus facillime flexilem.”[1]

“Now let this problem be proposed: To find the curve assumed by a loose thread hung freely from two fixed points. I also assume that the thread is a line which is easily flexible in all its parts.”

Bernoulli’s challenge was to find the curvature of a thread hanging by its ends, curved under its own weight.  He specifically says the thread is easily flexible in all its parts.

Many mention this as the start of the catenary challenge, which is the problem of finding the curvature of a hanging chain.  But the question Bernoulli raised is more complicated than finding the catenary curve. By not specifying any condition that limits the problem to the nonelastic case, he challenged the mathematicians of the time to find the shape of a hanging elastic rope. Bernoulli must have believed that if one finds the curvature for the elastic case, then that of the nonelastic case can be obtained, which means he intended to solve the generic Funicularia Problem (Alassi 2020). With this challenge, Jacob Bernoulli extended the practice of starting mathematical challenges by proposing the question to the entire mathematical community, not just a few mathematicians. He then especially requested Leibniz and Tschirnhaus (1651–1708) to consider the problem and use their new methods to solve it. Knowing the problem's difficulty, Bernoulli did not specify any deadline for the challenge.

Change from Funicularia to Catenaria Challenge

While Bernoulli was occupied with solving the Funicularia problem, in July 1690, Leibniz, who had just returned from a long trip, replied to Bernoulli’s challenge in AE. He wrote: "It should be assumed that the thread, like a chain, keeps the same length and is neither stretched nor shortened as a regular thread would do" (Leibniz 1690). Thus, he literally simplified Jacob’s challenge to solving the catenary problem.

Leibniz announced that although he had the solution to the catenary problem, he would allow others time to consider it because this problem reveals the exceptional applications of the Leibnizian calculus. If no one presented any solution by the end of the year, he would share his result with the public. Leibniz requested the answers to be skillful as the results were to be compared later. In addition, he specifically nominated Tschirnhaus to employ his new method to solve the catenary problem to prove its usefulness.

Unlike Bernoulli, who employed a requesting tone in asking Leibniz and Tschirnhaus to consider the problem, Leibniz uses a demanding tone. In this way, he stated his doubts about the generality and usefulness of Tschirnhaus’ method. Thus, Leibniz not only simplified Bernoulli’s challenge but also nominated someone to solve it and set a deadline for the challenge. From that time on, the participating mathematicians focused on finding the curvature of the Catenaria, all except Jacob Bernoulli, who remained with his original problem.

The first response to Leibniz’s challenge came from Christiaan Huygens on 9 October 1690.[2] This was the starting point of a correspondence between the two giants about the catenary problem. Huygens sent his solution to Leibniz as a cipher containing Eq. 1 and outlined that in his youth, he had corresponded with Father Mersenne (1588–1648) about this problem and had found that the curve of a hanging chain is not a parabola as Galileo (1564–1642)  had assumed.

$xxyy \propto a^4 - a^2 y^2$ Eq.1

In return, Huygens asked to see Leibniz’s solution as a cipher, suggesting that between themselves, they could reduce the one-year time mentioned by Leibniz. Huygens thought Leibniz had given one year's time, although it was just six months. The enclosed cipher contained the equation of the auxiliary curve for the geometric construction representing the catenary curve. In Huygens’ letter, we see the first appearance of an encrypted solution submitted for this challenge in a correspondence. He clearly writes:

This cipher conforms with the rules set in 1668 for anagrams and is very easy to decipher. The characters in the last line are the first letters of every word of the content in the correct order, with no shifting required. The first three lines of the anagram depict the properties of the catenary curve, which Huygens had found then, including the equation of the auxiliary curve. Leibniz immediately unraveled the cipher and found that it contained the equation of the auxiliary curve for the geometric construction of the catenary. On 13 October 1690, without enclosing any cipher, Leibniz replied that he had found some similarities with his calculation and a difference. The difference Leibniz points out is in the sign in the equation of the auxiliary curve.[3]

$$xxyy \propto a^4 + a^2 y^2$$

Huygens, who had checked his calculation and could not find any mistake in the sign of the auxiliary curve, had become suspicious of the accuracy of Leibniz’s calculation. On 18 November 1690, he requested to see Leibniz’s solution as a cipher to verify who had made a mistake.[4] This shows that Huygens was confident he could decode any anagram containing the solution to the catenary problem since he had the solution himself. In this letter, he also proposed the name Catenaria for the curve. Huygens also found an alternative auxiliary curve that could lead to a correct representation of the catenary curve. This indicates that he was perfecting his solution.

Meanwhile, Johann Bernoulli (1667–1748)  also solved the catenary problem and sent his solution directly to Mencke, the editor of AE, in December 1690. Johann set a condition for publishing his solution: he wanted it to be published simultaneously with Leibniz’s solution. Perhaps, he wanted readers to compare his solution with Leibniz’s easily and see how masterfully he had employed Leibnizian calculus. Mencke (1644–1707)  confirmed receiving this result in a letter to Leibniz on 6 January 1691 (Heß, Babin, 2011, 117, note 9). Johann had submitted his solution right before Leibniz’s deadline expired, but Leibniz did not publish his analysis; instead, he continued his correspondence with Huygens. Probably because he was still waiting to see if Tschirnhaus would take up the challenge. In a postscript of a letter sent to Huygens on 27 January 1691,[5] without enclosing any cipher of his own analysis, Leibniz accepted that Huygens’ auxiliary curve could also be used for the geometric construction of the catenary. The availability of many choices for an auxiliary curve representing the catenary must have convinced Huygens that the problem was not difficult to solve. On 23 February 1691,[6] he wrote to Leibniz: “I think there will be many other geometers who will solve this problem because, to tell you the truth, it does not seem very difficult, except that you ask for something more than what I have found” (Huygens, 1905, 22).

On 30th February 1691,[7] Leibniz informed Huygens that, in fact, Johann Bernoulli seemed to have succeeded in solving the problem and took pride in the idea that his calculus might have helped Johann. Admitting that his tone in nominating Tschirnhaus was not only demanding but deliberately provocative, Leibniz also expressed his disappointment at the fact that Tschirnhaus had not accepted the challenge. He wrote:

“Mr. Tschirnhaus didn’t bite, although I deliberately spoke in such a way as to draw him in, to allow him to use his method, since he had promised us that it would do so much, and had even indirectly reproached me for saying that ordinary analysis would not be sufficient in these cases”

On 26 March 1691,[8] Huygens, who had spotted a slip of the pen in his first cipher not related to the equation of the auxiliary curve though, sent Leibniz a second cipher that was a corrected and extended version of the first. Huygens suggested that Leibniz could communicate this second cipher to Johann and ask him for his in return. Still having the deadline wrongly in his mind, not noticing that the deadline was long passed, Huygens hoped that Tschirnhaus would come up with something in the remaining time. Moreover, in this letter, Huygens voices his opinion about the necessity of exchanging ciphers, namely to prevent any dispute and as a precaution to be sure that both sides of the communication are, in fact, in possession of the same solution. He also enclosed the key to his cipher in his letter mentioning that the anagram consisted of the first letters of words.

“… But to make the truth known about what one has found and to prevent any dispute, it is absolutely necessary to communicate the ciphers first, as I did a long time ago. I do not doubt that you and Mr. Bernoulli would agree that if, without this precaution, you first send him [Johann] your solution, you might suspect whether he is the author of his. Here is my cipher that I have put in a less embarrassing way than it was. It is scrutinized and facilitated by marking only the first letters of the words. I have also enclosed something more than the other.”

Huygens also sent this cipher to his friend Mr. De Beauval on 27 March 1691[9] and inscribed a complete account of the cipher and its content in an appendix for his personal record.

By sending the cipher to his friend, Huygens perhaps attempted to safeguard his priority by acquiring a witness for his discovery. Biagioli (2012, 216) believes that, at the time, it was preferred to send anagrams to key people spread over a wide geographic area.[10] 

On 21 April 1691, he informed Leibniz that he had found a few more properties of the catenary curve and that Mr. De Beauval now also possessed the cipher. Thus, even four months after the expiration of Leibniz’s catenary deadline, Huygens had continued to complete his analysis to such an extent that he confirmed: “There is nothing left to be found.” He, then, pestered Leibniz for his cipher one last time.[11]

As you can see, Huygens kept on improving his discovery. Since he had not received any anagram from Leibniz, albeit all his requests, he decided to take extra safety measures by sending his solution to one more person. In fact, it was preferred to send anagrams to key people spread over a wide geographic area at the time. Since Huygens’ cipher followed a very simple pattern and contained explicit equations, it was straightforward to decipher. Comparing this anagram to those Huygens had previously used on other occasions, it is evident that its simplicity is intentional, as he indicates in his first letter to Leibniz. Huygens believed that if Leibniz had the solution as he claimed, he could quickly decode the anagram anyway, so there was no need to make it complex.  After all, he had sent these ciphers in private correspondence to Leibniz not to announce a new discovery but to prove he also had a correct solution. Huygens wanted Leibniz to immediately understand the content of the anagram so that he would be announced as a winner of the catenary challenge. He felt the need to encrypt his solution because, first, he was not entirely sure Leibniz had the same solution, and second, to buy time to perfect his analysis. When he is satisfied with his analysis, he shares the key to decode the anagram with Leibniz, and a third party safely guards his discovery.

Jacob Bernoulli pursued the initial Funicularia Challenge

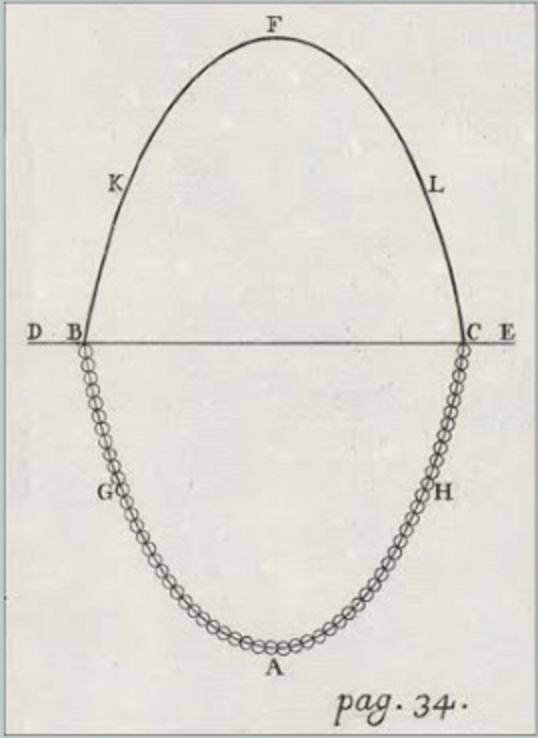
Meanwhile, Jacob Bernoulli, who had remained with his general Funicularia problem, urged Mencke, the editor of AE, to publish the solutions to the catenary problem in March 1691. He submitted an article that enclosed an appendix about the Funicularia problem. Jacob Bernoulli asserted that the catenary solutions could be generalized to other cases in this appendix containing four passages. In these passages, Bernoulli suggests the relation between the Catenaria and the Velaria (that is, the curvature of a sail inflated with the wind), as well as Lintearia (that is, the curvature of linen filled with water), and Elastica (that is the curvature of an elastic beam under a load).[12] In this appendix, Bernoulli explains the relations between these four curves meaning that they belong to the same family of curves.

Opposite to his brother, who was hasty in finding solutions and publishing them, Jacob normally took his time to formulate a comprehensive analysis covering as many properties and cases as possible. He explains the relations between the curves in this appendix. The generic mathematical equation for the entire family of curves, from which the equation of each of these four curves could be derived, is given in entry 245 of his scientific diary Meditationes.[13] On 21 March 1691, Mencke informed Leibniz about Jacob Bernoulli’s article (Heß, Babin, 2011, 117, note 10). They decided to publish it in the same issue containing the solutions to the catenary problem.

Publication of Catenaria Solutions

On 20 April 1691,[14] Leibniz notified Huygens that the editors of the AE were pressuring him to submit his answer. Reminding that the contest deadline was long expired, he informed Huygens that he would submit his analysis for publication soon and urged Huygens to do the same. On 5 May 1691,[15] Huygens sent his solution to Leibniz in a sealed envelope[16] along with a letter requesting his enclosed solution to be transmitted to AE. Together with it, Leibniz submitted his own solution for publication. In the June issue of AE 1691, Mencke published all three solutions to the catenary problem along with a preface that described the order and the date of the solutions. He placed Jacob Bernoulli’s article right after the three solutions. Later, these 4 articles were reviewed, and solutions were compared mainly to set standards for geometric construction by quadratures used to solve transcendental problems.

Start of a new Challenge: Elastica

The 3rd passage of Jacob Bernoulli’s appendix announced a new challenge to solve the Elastica problem: to find the curvature of an elastic beam fixed at one end, bent under the load attached to the other (Bernoulli 1691).

“…  I came across another amazing problem. It is about bending or the curvature of beams, drawn bows, or arbitrary elastic bands, caused by their own weight, a hanging weight, or any other bending force…. As the very famous man [Leibniz] has already done, I will also allow others some time to try to analyze this issue. Therefore, I will withhold the solution and hide it in a logogriph. By the harvest festival, I will publish the solution and proofs.”[17]

Bernoulli announced that he already possessed the solution, and following in Leibniz’s footsteps, he announced his discovery as a challenge, giving others time to consider the problem. But unlike Leibniz, Bernoulli offered his solution as a logogriph where the main property of the curve was hidden in the following puzzle:

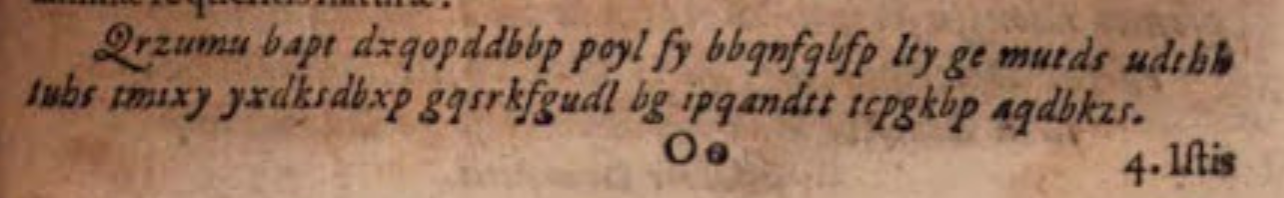
He did not nominate anyone in particular but invited those who had considered the catenary problem to try and solve this one too. He set a deadline for this challenge, namely the next harvest festival in which he would publish his solution and proofs.

By presenting this anagram, Bernoulli announced that he had made a discovery and bought himself time to perfect it. Since the harvest festival in Basel is in September, he essentially allowed himself three months to complete his analysis and others to solve the problem. However, since nobody stepped forward with a solution, Bernoulli took his time; he published his answer three years later, in 1694. During these years, Jacob was perfecting his solution, as seen from the entries in his scientific notebook Meditationes. He found around fifty properties of the curve before publishing his discovery in June 1694.[18] In this article, he gave the key to solving the puzzle:

“Explanation of the extended logogriph exists in three previously given alphabets. They should be chosen in alternation to bring out the secret hidden in the set of alphabets. For example, “a” would first respond to “b,” second to “d,” and third to “g.” I connect the remaining elements in ascending order. In this way, it is not difficult to uncover the logogriph itself and the proportions it contains” (Bernoulli 1694, p.272). 

At first glance, Jacob Bernoulli’s anagram may seem very difficult to decode. No one could decipher it until Bernoulli published its key three years later. The key describes that three stages of shifting the alphabet are required to solve the puzzle.

We should remember that Bernoulli used old Latin alphabets, excluding j, v, and w. Table 1 depicts the three stages of shifting alphabets, as Bernoulli described. This Table helps with keeping track of shifting the alphabet to the right. The row with label 1 represents one shift to the right, the one with label 2 represents three shifts, and the last with label 3 represents five shifts to the right. Next, I will illustrate an easy way of deciphering the anagram through Table 1.

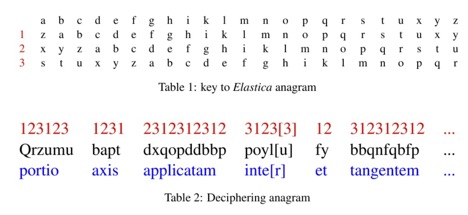
Firstly, we should note that the anagram contains a few minor mistakes:

●      The letter u in the term poyl[u] was missing in the original publication of the anagram in June 1691.

●      In the term mutds, the letter u should be x.

●      In the term ipdandtt, the letter n should be u.

Cramer (1746, 452) added the missing letter to the reprint of Bernoulli’s article but did not correct other mistakes. Historians of science who have studied this anagram, such as Truesdell (1960, 95) and Heyman (1999, 59), have not mentioned these mistakes. Heyman (1999, 59) even falsely assumes the content of the anagram to be about the inverse relation of the bending moment to the radius of curvature. After fixing the mistakes in the anagram, we can decode it, as shown in Table 2. The anagram is given in the second row of Table 2 in black; if we label each character periodically with 1,2,3, as shown in row 1, for each character, we can find the one corresponding to it from Table 1, the decoding result is shown in the third row in blue. The decoded content is the key property of the Elastica curve, namely that the subtangent of the curve to its tangent is as the square of its ordinate to some constant.

The errors in Bernoulli’s anagrams are minor, and the cipher is based on an algorithm of average complexity. When starting the challenge, Bernoulli mentions that the solution is in a logogriph; hiding the solution in a puzzle would entice the reader to try at least deciphering the anagram. Even if someone did not have the solution to the Elastica problem, Bernoulli’s discovery would have been revealed by finding out the algorithm. Therefore, I believe Bernoulli’s cipher was meant to be decoded with a certain amount of effort. Not every natural philosopher intended to publish anagrams with such a simple algorithm; let’s look at another set of anagrams by Hooke.

Anagrams in Hooke’s Publications

Hooke’s ciphers are nearly impossible to decipher without knowing the content. In the heat of a dispute with Huygens, Hooke communicated his various discoveries as anagrams printed in an appendix to his book A Description of Helioscopes. Thus, he bypassed the Royal Society's registering system (which he had come to distrust) and the possibility of seeing his discoveries made public before publication by porous print shops or talkative journal editors. At the end of this appendix, we find a list of discoveries, four of which are given as anagrams.[19]

Hooke revealed two of these anagrams in his later publications, the others he left encrypted. All anagrams are in old Latin, i.e., u is used instead of v. Two of these anagrams are related to the topics discussed earlier:  one of them (number 3) is Hooke’s law of linear elasticity which was used to solve the Elastica Problem even though this law was known in the continent as Leibniz’s theorem. In modern terminology, the strain is proportional to the stress.

ceiiinosssttuu:

ut tensio sic vis

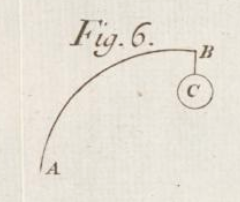
The other (number 2) is about the nature of catenary arches. A masonry arch with an inverse catenary curve in its center line is the most stable; see Figure below.[20]

abcccddeeeeefggiiiiiiiillmmmmnnnnnooprrsssttttttuuuuuuuux

Ut pendet continuum flexile, sic stabit continguum rigidum inversum

In 1671, Hooke announced to the Royal Society that he had solved the problem of an optimal arch. He added his solution as an anagram in the margin of this book, published in 1675; its deciphered form means: As hangs the flexible line, so but inverted will stand the rigid arch. This finding remained encrypted for decades; Hooke never published his analysis and decoded form of the anagram.

Contrary to Bernoulli’s anagram, Hooke’s ciphers seem not to be based on an algorithm. The only pattern they seem to follow is that the letters are given alphabetically as often as they are used in the phrase. Thus, in my opinion, Hooke, who believed in privatizing knowledge, had encrypted his discoveries in this very secure style and published them in his book to register them. They were not meant to be decoded by anyone else until Hooke rejoined the content with its certified temporal origin. 

Natural philosophers like Leonhard Euler (1707–1783) continued using ciphers in the 18th century.  

Ciphers in Euler’s Correspondence

Ciphers appear in other historical, scientific documents; a quick search for the term cipher or logogriph in the Bernoulli-Euler Online platform[21] shows multiple letters containing one of these two terms in Euler's correspondence. For example, in a letter that Leonhard Euler sent to Christian Golabch (1690-1764)  on the 4th of July 1744,[22] he gives a logogriph he had created using his new encryption algorithm, which he believes cannot be deciphered that easily. There is no evidence whether Goldbach, a Prussian mathematician and the Russian Foreign Office's cryptographer at the time, could solve this cipher. However, a historian of science, Pierre Speziali (1953), decoded Euler’s cipher in 1953 by applying frequency analysis. This logogriph's content is not scientific but a passage from Julius Caesar’s De bello Gallico. This letter shows Euler’s interest in cryptography and designing encryption algorithms. There are other letters in Euler-Goldbach correspondence containing ciphers, but they are mainly for military purposes, not hiding scientific discoveries.[23] Other natural philosophers continued using ciphers in the 18th century, which are left to be studied. 

Note: for an extended study of this topic and Bernoulli's study of the Funicularia family of the curves, see Chapter 1, Alassi 2021.

[1] Bernoulli Jacob, 1690, p.219.

[2] Lettre No. 2623, Christiaan Huygens à G. W. Leibniz, A la Haye ce 9 Octobre 1690 (Huygens, 1901, p.497).

[3] Letter. No. 2627, G. W. Leibniz à Christiaan Huygens, 13 Octobre 1690 (Huygens, 1901, 518).

[4] Lettre No. 2633, Christiaan Huygens à G. W. Leibniz, Leibniz, 18 Novembre 1690 (Huygens, 1901, 537).

[5] Nr. 2659, G. W. Leibniz `a Christiaan Huygens, Hanover ce 27 de Janvier 1691. The transcription has the date of arrival, 6 F´evrier 1691 (Huygens, 1905, 9-16).

[6] Lettre Nr. 2660, Christiaan Huygens `a G.W. Leibniz, A la Haye 23 F´evrier 1691. (Huygens, 1905, 17-22).

[7] Lettre No.2664, G. W. Leibniz `a Christiaan Huygens, Hannover ce 20/30 F´evrier 1691. The letter was written at the end of February, but its copy in Huygens correspondence series contains the date it was received, 2 Mars1691 (Huygens, 1905, 49-52).

[8]Lettre No. 2667, Christiaan Huygens `a G. W. Leibniz, A la Haye 26 Mars 1691 (Huygens, 1905, 55-58).

[9] Nr. 2668, Christiaan Huygens 1691. Appendice I au No. 2667. Chifre envoié à Mr. Leibniz le 26 Mars 1691 et à Mr. De Beauval le Mars 27 (Huygens, 1905, 59-62).

[10] Biagioli 2012.

[11] (Huygens, 1905, 86) 

[12] For the study of Bernoulli's analysis of the four curves of the Funicularia family, see Alassi 2020.

[13] https://ark.dasch.swiss/ark:/72163/1/0801/ZSMQ_f_mTP6vZ_=qrSCT8Qw.201910...

[14] Lettre No. 2676, G. W. Leibniz `a Christiaan Huygens, A Hanover ce 10/20 d’Avril 1691 (Huygens, 1905, 83-86).

[15] Lettre Nr. 2680, Christiaan Huygens `a G. W. Leibniz, A la Haye ce 5 Mej 1691 (Huygens, 1905, 93-94).

[16] Letter No. 2681, Christiaan Huygens aux ´editeurs des Acta Eruditorum, 5 Mai 1691 (Huygens, 1905, 95-98).

[17] Bernoulli Jacob, 1691. 

[18] Bernoulli Jacob 1694.

[19] Hooke 1675, p. 6.A.

[20] Poleni, 1748.

[21] https://beol.dasch.swiss/

[22] https://ark.dasch.swiss/ark:/72163/1/0801/4ZPxVMKWQfivQKUdGppDuwv.201910...

[23] You can find the digital edition of the Euler-Goldbach correspondence in the BEOL platform https://beol.dasch.swiss/

Alassi, Sepideh “Jacob Bernoulli’s Analyses of the Funicularia Problem”. British Journal for the History of Mathematics. 2020. vol 35 (2), p.137-161.

Alassi, Sepideh "From the Mechanics of Jacob Bernoulli to Digital History of Science. Infrastructure, Tools, and Methods", 2021.

Bernoulli Jacob. Analysis Problematis antehac propositi, de inventione lineae descensus a corpore gravi percurrendae uniformiter, sic ut temporibus aequalibus aequales altitudines emetiatur: & alterius cujusdam Problematis Propositio // Acta Eruditorum. 1690. Maji. 217–219. 

Bernoulli Jacob. Specimen alterum Calculi differentialis in dimetienda Spirali Logarithmica, Loxodromiis Nautarum, &; Areis Triangulorum Sphaericorum: una cum Additamento quo- dam ad Problema Funicularium, aliisque // Acta Eruditorum. 1691. Junii. 282–290. 

Bernoulli Jacob. Curvatura laminae elasticae // Acta Eruditorum. 1694. Junii. 262–276. 

Biagioli Mario. From ciphers to confidentiality: secrecy, openness and priority in science // BJHS. 2012. 45, 2. 213–233. 

Burke R. B. Roger Bacon // Proceedings of the American Philosophical Society. 1927. 66. 79–88. 

Cramer Gabriel (ed.). Jacobi Bernoulli Opera Omnia. 1746. Golinski Jan. Making Natural Knowledge: constructivism and the history of science,... 2005. 

Heß Heinz-Ju ̈rgen, Babin Malte-Ludof.  Die Mathematischen Zeitschriftenartikel, Gottfried Wilhelm Leibniz. 2011. 

Hooke Robert. A Description of Helioscopes, and some other instruments. 1675.

Huygens Christiaan. Oeuvres complètes de Christiaan Huygens. Publiées par la Société hol- landaise des sciences. IX: Correspondence 1685-1690. 1901.

Huygens Christiaan. Oeuvres complètes de Christiaan Huygens. Publiées par la Société hol- landaise des sciences. X: Correspondence 1691-1695. 1905.

Huygens Christiaan. Oeuvres complètes de Christiaan Huygens. Publiées par la Société hol- landaise des sciences. XIX. 2002. 

Iliffe Rob. “In the Warehouse”: Privacy, Property and Priority in the Early Royal Society // History of Science. 1992. 30(1). 2968. 

Leibniz Gottfried Wilhelm. Ad ea, quae vir clarissimus J. B. mense Majo nupero in his Actis publicavit, responsio. // Acta Eruditorum. 1690. Juli. 358–369.

Leibniz Gottfried Wilhelm. De Linea in quam flexile se pondere proprio curvat ejusque usu in- signi ad inveniendas quotcunque medias proportionales & Logarithmos. // Acta Eruditorum. 1691a. Junii. 277–281. 

Speziali, Pierre   “Le logogriphe d’Euler”, "Stultifera navis" (Bulletin de la Société suisse des bibliophiles), 1953, n.10, p.6-9.

Truesdell Clifford. The Rational Mechanics of Flexible or Elastic Bodies. 1960.